The ways we count numbers are far more diverse than we typically think. As humans, we naturally use the decimal system (base 10) because we have ten fingers, but computers think in an entirely different language. That language is called Binary. In this blog, we'll explore everything from the fundamental principles of how computers handle numbers to the real-world problems of Base conversion encountered in development and their solutions. You can follow along and practice using our Number Base Converter tool.
Why Do Computers Use Binary?
This is one of the most fundamental yet core questions in computer science. The answer is simple but rooted in deep physical principles.
The inside of a computer consists of millions of transistors, and each transistor can only have two states: ON and OFF. When we represent these two states as 1 and 0 respectively, binary naturally emerges. GeeksforGeeks's Number System guide also emphasizes that binary is the fundamental foundation of digital systems.
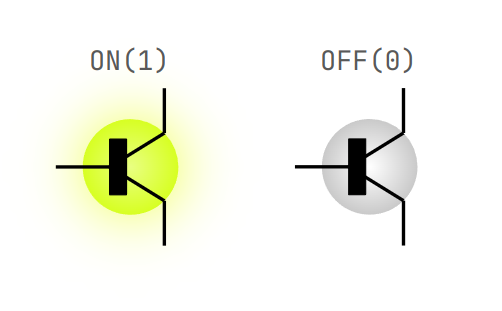
The correspondence between transistor ON/OFF states and binary
For example, to simply store the number 5 in a computer, it must be represented in binary as 101. The larger the number, the longer the binary representation becomes, which is where Octal (base 8) and Hexadecimal (base 16) come in to solve binary's readability problem.
Four Number Systems: Their Roles and Uses
There are four main number systems used in the computer world. Understanding each of their roles reveals that Base conversion isn't just about changing numbers—it's about changing perspectives.
| Base | Name | Digits Used | Typical Use Cases |
|---|---|---|---|
| 2 | Binary | 0, 1 | Computer internal operations, circuit design |
| 8 | Octal | 0–7 | Unix file permissions, early computing |
| 10 | Decimal | 0–9 | Daily life, user interfaces |
| 16 | Hexadecimal | 0–9, A–F | Memory addresses, color codes, debugging |
Hexadecimal: The Programmer's Secret Weapon
When I first started web development, I had no idea what the CSS color code #FF5733 meant. When I later learned that this represents Red=FF(255), Green=57(87), Blue=33(51), expressing each color's intensity in hexadecimal, I truly appreciated the power of hex for the first time.
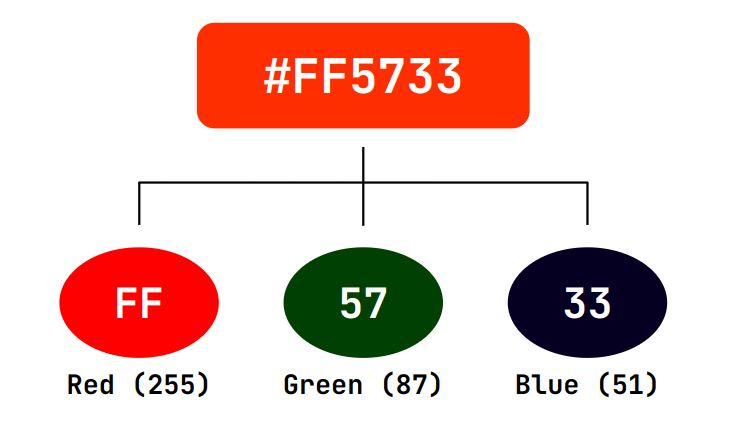
Breaking down the RGB components of a hexadecimal color code
The reason hexadecimal is so commonly used in programming is because it has a perfect mapping relationship with binary. One hexadecimal digit corresponds exactly to four binary digits (a nibble). SparkFun's Hexadecimal tutorial also emphasizes this relationship, explaining that one byte (8 bits) can always be concisely represented with two hexadecimal digits.
I truly benefited from this advantage when reading hardware sensor register maps. An address like 0x21 is immediately comprehensible, but viewing it in binary as 00100001 makes finding errors much more difficult.
The Mathematical Principles of Base Conversion
Base conversion may look complex, but its foundation is one simple principle: Positional Notation.
Any number
For example, converting the hexadecimal number 2A3 to decimal:
Based on this principle, conversion methods are broadly divided into two types:
Decimal → Other Base: Perform repeated division by the target base and read the remainders in reverse order. For example, to convert 71 to binary: 71÷2=35 remainder 1, 35÷2=17 remainder 1, 17÷2=8 remainder 1, 8÷2=4 remainder 0, 4÷2=2 remainder 0, 2÷2=1 remainder 0, 1÷2=0 remainder 1. Reversing the remainders gives 1000111.
Other Base → Decimal: Apply the positional notation formula described above directly.
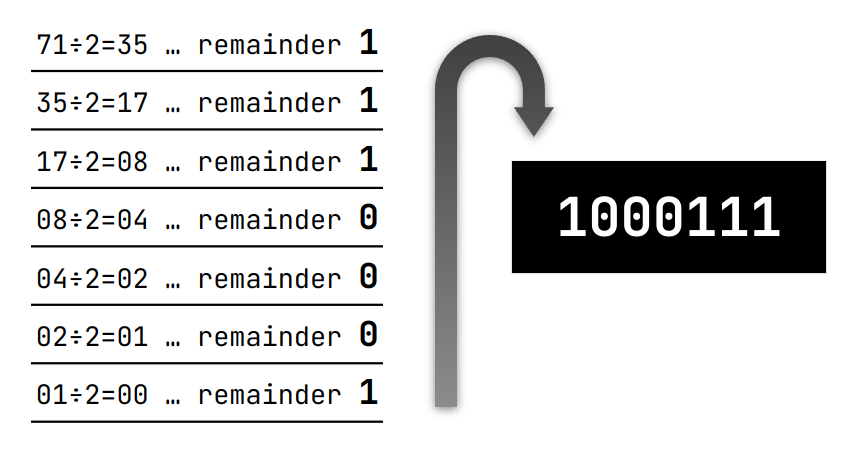
Step-by-step process of converting decimal 71 to binary
Number Base Converter Tool Usage Guide
Once you understand the mathematical principles, manually calculating these conversions in actual work isn't efficient. This is where the Number Base Converter tool shines.
Real-World Scenario: Color Debugging During Android App Development
This is a situation I personally experienced. The color specification I received from the designer was RGB values (201, 58, 30), but Android's xml requires color codes in hexadecimal format.
- Input in the tool page: Enter the decimal value
201in the input field.
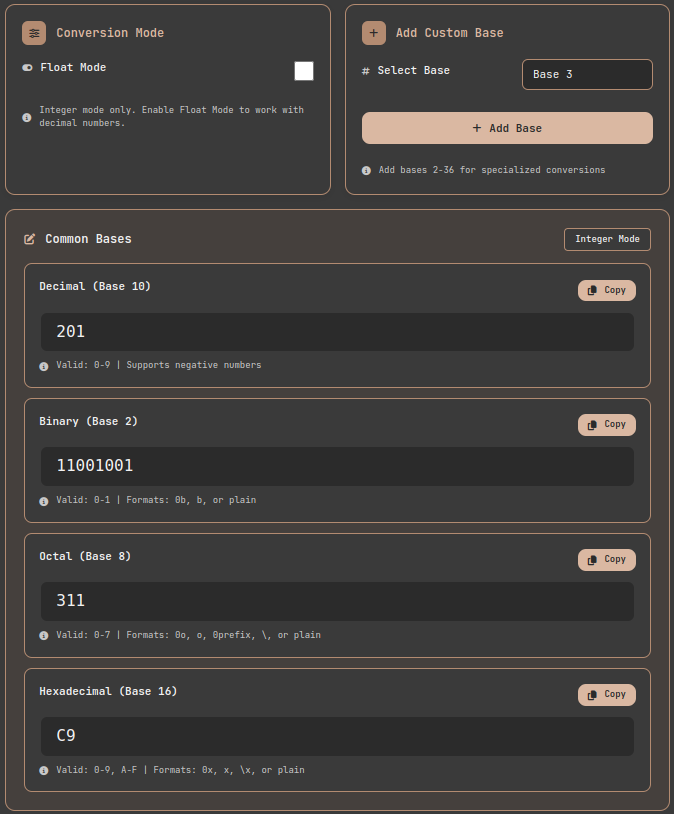
Number Base Converter tool: Input interface and real-time conversion
-
Check real-time conversion: The Hexadecimal field automatically displays
C9. -
Convert all three colors: Using the same method,
58→3A,30→1E, resulting in the final color code#C93A1E. -
Use custom bases: Using the tool's "Add Base" feature, you can instantly convert special bases like Base 23 or Base 32.
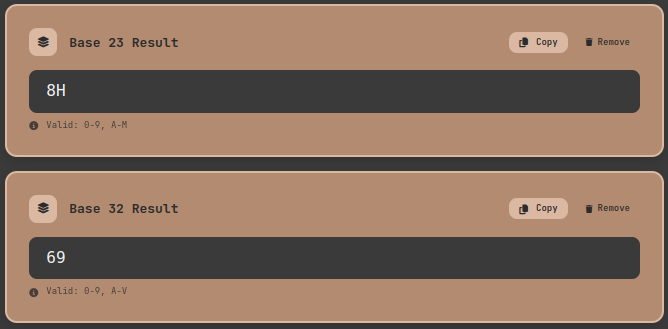
Number Base Converter tool: Custom base addition feature
Floating-Point: The Real Challenge of Base Conversion
Integer conversion is straightforward, but when we move to floating-point numbers, the problem becomes much more complex. This was the topic that confused me most when I first studied computer science.
Why? Because the number 0.1, which we use without a second thought, cannot be represented exactly in computers.
Why Isn't 0.1 Exact?
Computers store numbers as binary fractions. Just as 1/3 = 0.333... repeats infinitely in decimal, 0.1 in binary is 0.0001100110011... repeating infinitely. Python's official documentation on floating-point also clearly addresses this issue. Since computers must truncate this infinite repetition with a finite number of bits, there's always some approximation error.
To standardize this problem, the IEEE 754 standard was established in 1985. The historical background of the IEEE 754 standard shows that this standard is now used in billions of processors, including smartphones.
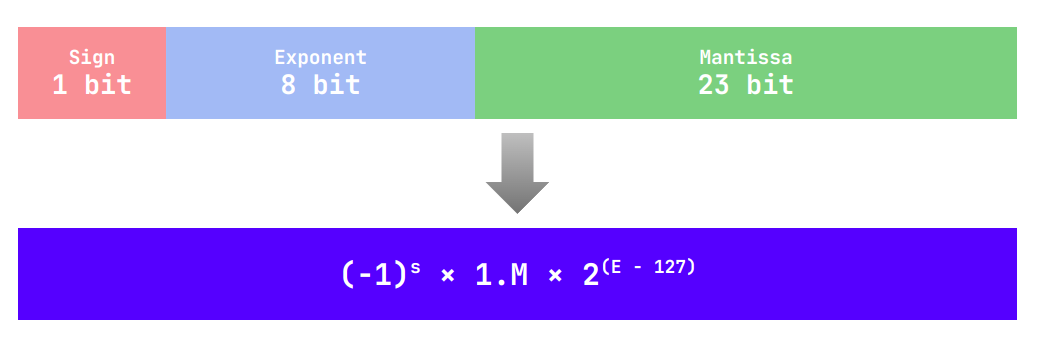
IEEE 754 single precision (32-bit) floating-point structure
IEEE 754: The International Standard for Floating-Point
IEEE 754 divides floating-point numbers into three parts:
- Sign bit: 1 bit — positive (0) or negative (1)
- Exponent: 8 bits in single precision (float) — determines the magnitude (scale) of the number
- Mantissa/Significand: 23 bits in single precision — determines the actual precision of the number
Using the same principle as scientific notation in binary, numbers are normalized to the form
Single precision (32-bit) provides about 7 decimal digits of precision, while double precision (64-bit) provides about 16 digits.
Representing Repeating Decimals: Practice with the Tool
When you activate Float Mode in the Number Base Converter, you can witness this phenomenon firsthand. For example, converting the decimal 0.333... (the result of 1 divided by 3) to binary:
The tool represents such repeating decimals in the form 0.333(3), making it easy to see which part repeats. When I first built this feature, I realized that repetition patterns in binary are far more complex than expected. As the base increases, the repetition cycle becomes longer, making patterns harder to identify.
Real Development Experience: Errors and Solutions
Equally important as theoretical understanding is experiencing the problems that Base conversion and floating-point cause in actual projects.
Experience 1: Precision Issues in Financial Calculations
In my first project, I had a task to implement a simple financial calculator. I wrote the following code in Python:
I was flustered when this simple addition returned an inaccurate result. After understanding the fundamental limitations of floating-point, I learned that financial calculations must always use Decimal types or integer units (e.g., cents).
Experience 2: Color Code Discrepancy in Android App
This was the color debugging situation I mentioned earlier. The color from the designer's Figma file and the color displayed in the actual app were subtly different, and I couldn't find the cause for dozens of minutes. Finally, by directly verifying RGB values and Hex codes using the Number Base Converter, I discovered that the error arose from inconsistent methods of sharing color specs within the team. We subsequently established a rule to always share colors based on Hex codes.
Experience 3: IPv6 Address Debugging
When working on a network engineering project, understanding the format of IPv6 addresses itself was a major barrier. IPv6 addresses are 128 bits represented in hexadecimal as 2001:0db8:85a3:0000:0000:8a2e:0370:7334, which expands to 128 digits in binary. In such cases, the Number Base Converter's custom base feature and real-time conversion significantly improved my work speed.
Performance and Practical Advice
One reason Base conversion doesn't end as merely an academic topic is performance. Choosing the wrong number type in programming languages and frameworks incurs unnecessary conversion costs.
Use integers when you can use integers. Floating-point operations cost more computationally, and precision errors accumulate.
Avoid unnecessary type conversions. For example, converting Hex → Decimal → Binary twice is less efficient and more error-prone than converting Hex → Binary directly. Direct conversion between binary and hexadecimal is very fast because each hexadecimal digit maps to a 4-bit binary block.
Be careful with floating-point comparisons. When comparing whether two float values are equal, don't use the == operator directly; instead, compare with a tolerance (epsilon):
Conclusion: Understanding the Language of Numbers Reveals the Computer
Base conversion is one of the most basic concepts in computer science, but understanding it properly solves many mysteries of programming. Why color codes are 6 digits, why memory addresses start with 0x, why 0.1 + 0.2 isn't 0.3 — all of this comes down to the principles of Base and floating-point.
Practice is the best teacher. Open the Number Base Converter tool, enter numbers, and directly observe the conversion results. When the relationships between binary, octal, decimal, and hexadecimal become visibly apparent, that's the moment you've understood the essential principles of Base conversion.
Additional Learning Resources
- GeeksforGeeks — Number System & Base Conversions — A systematic guide to conversions from binary to hexadecimal
- Python Official Documentation — Floating-Point Arithmetic Issues — The clearest explanation of floating-point's fundamental limitations
- SparkFun Learn — Hexadecimal Tutorial — An introductory guide to hexadecimal from a practical perspective
- GeeksforGeeks — Floating Point Representation Basics — Visual explanation of IEEE 754 structure and operating principles