Rotating objects in 3D space. It sounds simple enough, but this is actually one of the most fundamental yet challenging problems in modern 3D technology. The reason game characters move smoothly, drones fly stably, and robotic arms precisely grasp objects all comes down to handling rotation transformations correctly. In this article, we'll explore the three core rotation representations, the real-world problems you'll encounter, and how to solve them. If you want to calculate and visualize rotation transformations yourself, check out the 3D Rotation Converter tool.

The Beginning: Why Is Rotation So Complicated?

When I first started 3D programming, I thought rotation was simply a matter of "rotate 30 degrees around X, then 45 degrees around Y." But when I implemented inverse kinematics for a robotic arm in a real project, reality hit hard. The arm worked perfectly in simulation, but in the real environment, it would suddenly jitter or rotate in unexpected directions when reaching certain poses. After days of debugging, I discovered the culprit: Gimbal Lock—a fundamental limitation of certain rotation representations.

This experience taught me an important lesson. 3D rotation isn't just about three angles—the mathematical representation you choose completely determines stability, performance, and implementation complexity.

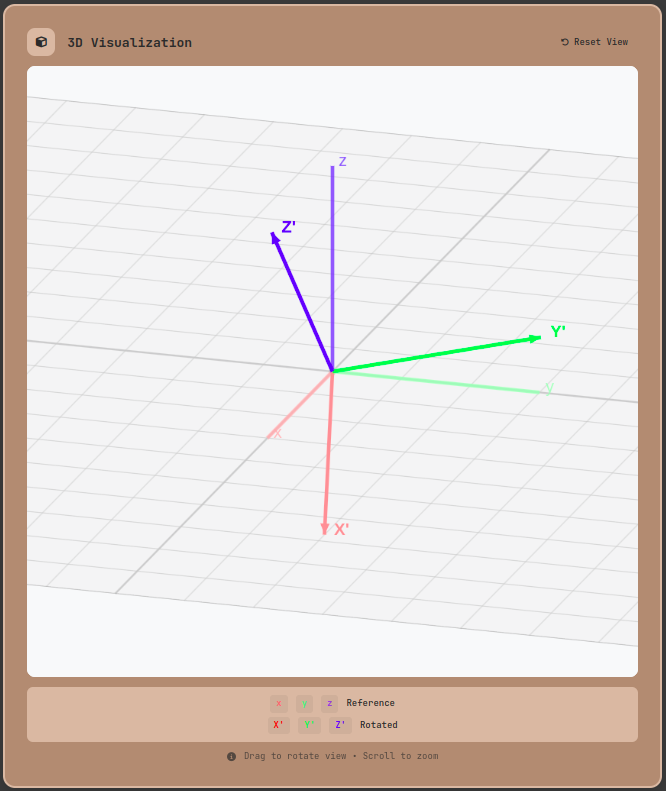
The basic concept of 3D rotation: Reference coordinate axes (red, green, blue) and the transformed axes (X', Y', Z') after rotation

First Encounter: The Intuitive Appeal and Hidden Pitfalls of Euler Angles

Euler Angles are typically the first rotation representation developers encounter. Open any 3D software like Blender, Unity, or Maya, and the first thing you'll see are Rotation X, Y, Z input fields. This intuitiveness makes them seem like the perfect choice for beginners.

An Intuitive Representation

Think about an aircraft's orientation:

• Roll (X-axis rotation): Tilting side to side
• Pitch (Y-axis rotation): Nose moving up or down
• Yaw (Z-axis rotation): Turning left or right

Euler Angles are easy to understand and convenient for direct manipulation. When rotating an object in a game editor, you can instantly decide "I need to rotate 90 degrees around Y" without any extra thought.

But Danger Lurks Beneath

The problems begin when you actually start computing. Euler Angles have two critical pitfalls.

First: Gimbal Lock

When certain angles are reached (typically when Pitch hits ±90 degrees), two rotation axes align and you lose one degree of freedom. This isn't just a theoretical concern—it's a documented historical event. During NASA's Apollo 11 mission, temporary attitude control issues due to Gimbal Lock were reported.

I faced this exact problem while working on a drone control project. The drone flew perfectly in level flight, but when aggressive maneuvers brought the Pitch angle close to 90 degrees, control suddenly became unstable. The sensor values were fine, but one degree of freedom had vanished in the Euler Angles calculation.

Second: Rotation Order Dependency

"90 degrees around X, then 90 degrees around Y" produces a completely different result than "90 degrees around Y, then 90 degrees around X." This is why you must always specify rotation order in practice:

• Aerospace: ZYX order (Yaw → Pitch → Roll)
• ROS Robotics: XYZ order (RPY) by default
• Unity Game Engine: ZXY internal representation

The same values "30, 45, 60 degrees" yield different results depending on order. This causes major confusion during team collaboration and library integration.

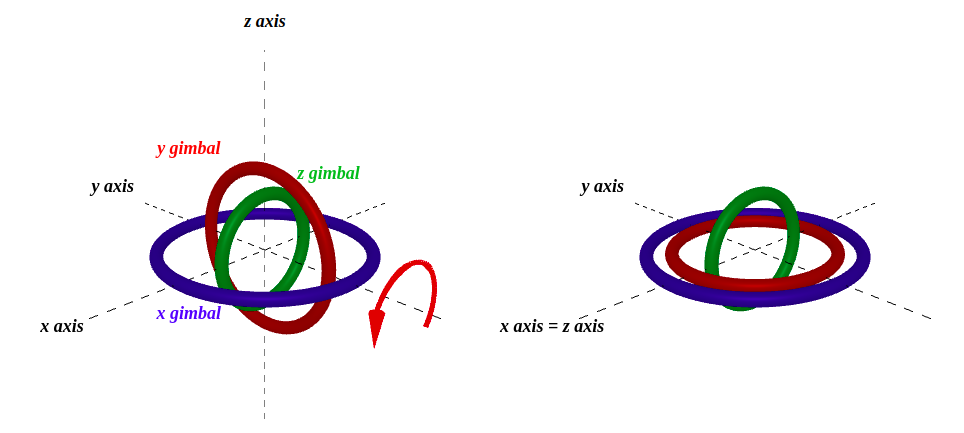
Gimbal Lock: When Pitch reaches 90 degrees, the Yaw and Roll axes align, losing one degree of freedom

The Turning Point: Quaternions as the Solution

After experiencing the limitations of Euler Angles, I first encountered the concept of Quaternions. Honestly, at first, neither the idea of representing 3D rotation with four numbers nor the explanation about extending complex numbers to three dimensions made any sense. But after actually applying them, I finally understood. Quaternions aren't just another representation—they're a mathematical structure that captures the essence of rotation.

The Essence of Quaternions

Discovered by William Rowan Hamilton in 1843, Quaternions represent rotation using four values $(x,y,z,w)$. Mathematically:

$$q=w+xi+yj+zk$$

where $i^2=j^2=k^2=ijk=-1$. A unit quaternion satisfies $|q|=\sqrt{w^2+x^2+y^2+z^2}=1$.

More intuitively, rotation by angle $\theta$ around axis $\overrightarrow{v}=(v_x,v_y,v_z)$ is expressed as:

$$q=\cos (\theta /2)+\sin (\theta /2)(v_{x}i+v_{y}j+v_{z}k)$$

It looks complex at first, but the key insight is that rotation is represented as a combination of rotation axis and rotation amount.

A Dramatic Difference in Practice

Let's return to the drone project. After switching from Euler Angles to Quaternions:

1. Complete elimination of Gimbal Lock: Stable control in all orientations
2. Improved sensor fusion: Implemented the Madgwick filter algorithm with Quaternions for more accurate IMU sensor data processing
3. Smooth animation: Used SLERP (Spherical Linear Interpolation) for the most natural rotation path when transitioning to target orientations

SLERP in particular is revolutionary for game development. When a character turns to look behind, Euler Angles create awkward intermediate frames, but Quaternion SLERP always finds the shortest rotation path for smooth movement:

// Unity C# example
Quaternion smoothRotation = Quaternion.Slerp(
    currentRotation, 
    targetRotation, 
    Time.deltaTime * rotationSpeed
);

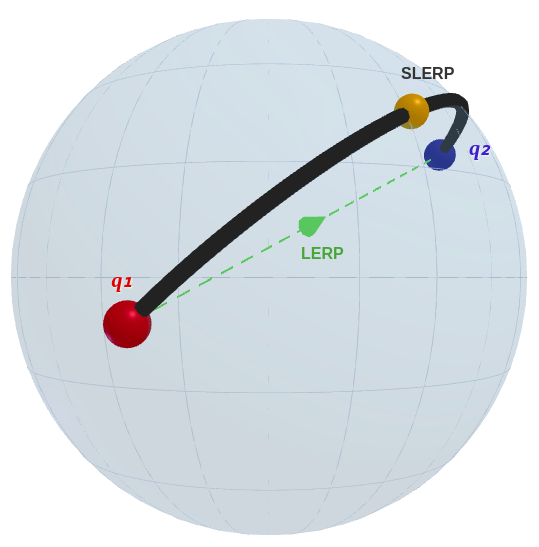
SLERP (Spherical Linear Interpolation): Smooth interpolation along the shortest path on the 4D unit sphere between two rotation states

Why It Became the Industry Standard

Today, virtually all modern 3D systems use Quaternions internally:

• Game Engines: Both Unity and Unreal Engine use Quaternions for internal rotation representation
• Robotics: ROS's tf2 library handles all transformations with Quaternions
• Aerospace: The International Space Station (ISS) uses quaternion-based attitude control, NASA's standard for stable orientation control without Gimbal Lock in space environments. (NASA ISS Attitude Control Document)
• AR/VR: Both ARKit and ARCore provide camera poses as Quaternions

This is no coincidence. Quaternions offer overwhelming advantages in stability, efficiency, and accuracy.

The Third Option: The Practicality of Rotation Matrices

There's another way to represent rotation: the 3×3 Rotation Matrix. Using 9 values seems inefficient, but in certain situations, it can be the best choice.

The Power of Linear Algebra

A rotation matrix $R$ satisfies these properties:

$$R^{T}R=I,det(R)=1$$

Rotating point $\overrightarrow{p}$ is simply matrix multiplication:

$$\overrightarrow{p^{\prime }}=R\overrightarrow{p}$$

When to Choose Matrices?

I was working on camera calibration for a computer vision project. OpenCV's solvePnP function returns rotation as a Rodriguez vector, and converting it for 3D rendering required transformation. Using Rotation Matrices as an intermediate representation made everything clean and organized.

When Matrices Are Advantageous:

1. GPU Optimization: OpenGL and DirectX use 4×4 transformation matrices directly
2. Composite Transformations: Combine rotation, scale, and shear into a single matrix
3. Multiple Rotation Composition: Handle with a single matrix multiplication

In graphics pipelines, a hybrid approach is common: compute with Quaternions on the CPU, then convert to Matrices when sending to the GPU.

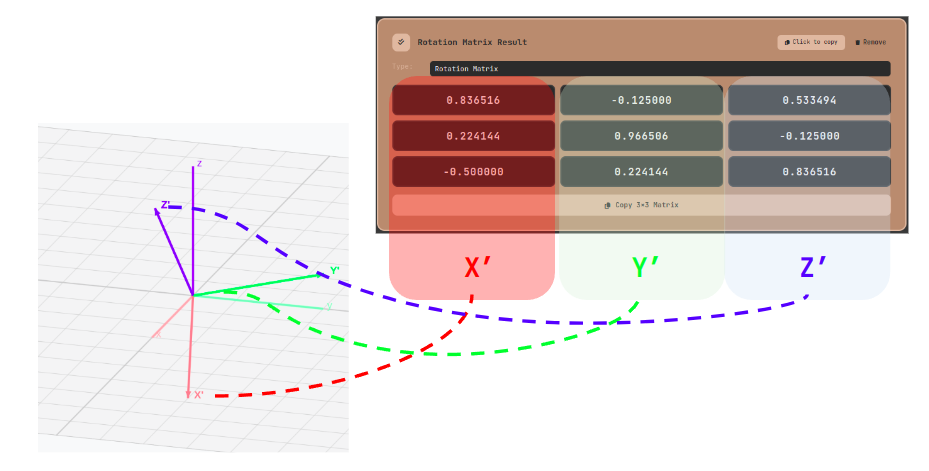
Geometric interpretation of a rotation matrix: The three column vectors represent the X', Y', Z' axis directions after rotation

Practical Application: Converting Between the Three Representations

Now that you understand the theory, you need to know how to convert and apply them in practice. Working with different libraries and frameworks across projects made me realize just how important conversion is.

Mathematical Foundation of Conversions

Euler Angles to Quaternion (ZYX order):

$$\begin{array}{rl}{q}_w& =\cos (\varphi /2)\cos (\theta /2)\cos (\psi /2)+\sin (\varphi /2)\sin (\theta /2)\sin (\psi /2)\end{array}$$ $$\begin{array}{rl}{q}_x& =\sin (\varphi /2)\cos (\theta /2)\cos (\psi /2)-\cos (\varphi /2)\sin (\theta /2)\sin (\psi /2)\end{array}$$ $$\begin{array}{rl}{q}_y& =\cos (\varphi /2)\sin (\theta /2)\cos (\psi /2)+\sin (\varphi /2)\cos (\theta /2)\sin (\psi /2)\end{array}$$ $$\begin{array}{rl}{q}_z& =\cos (\varphi /2)\cos (\theta /2)\sin (\psi /2)-\sin (\varphi /2)\sin (\theta /2)\cos (\psi /2)\end{array}$$

Quaternion to Euler Angles uses the atan2 function, but requires special handling near Gimbal Lock.

Practical Workflow Using Tools

The 3D Rotation Converter lets you verify these conversions in real-time. Let's walk through a real-world example.

Scenario: Transferring Data from a ROS Robot to Unity Simulation

You need to visualize a robotic arm's current pose in Unity.

1. Receive data from ROS: Quaternion format (e.g., x=0.0, y=0.707, z=0.0, w=0.707)

2. Configure 3D Rotation Converter:

   • Input settings: Select Type as "Quaternion"
   • Output settings
     • Type: Select "Euler Angles"
     • Unit: "Degree" (Unity uses degrees)
     • Order: "ZXY" (Unity's internal representation)
     • Click "Add Output" button
   • Enter the received values

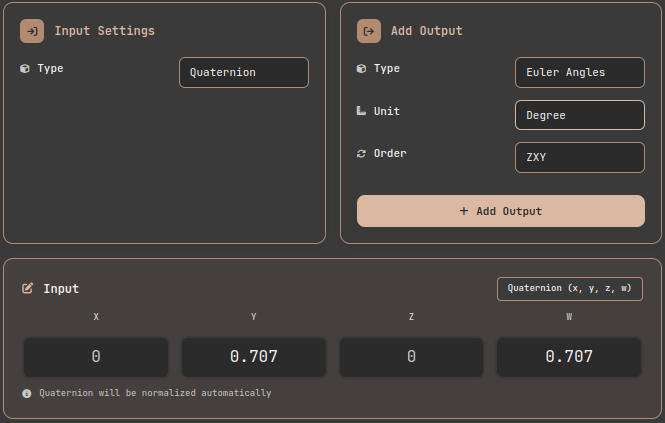
3D Rotation Converter tool: Input settings and interface

3. Verify rotation direction with 3D visualization:

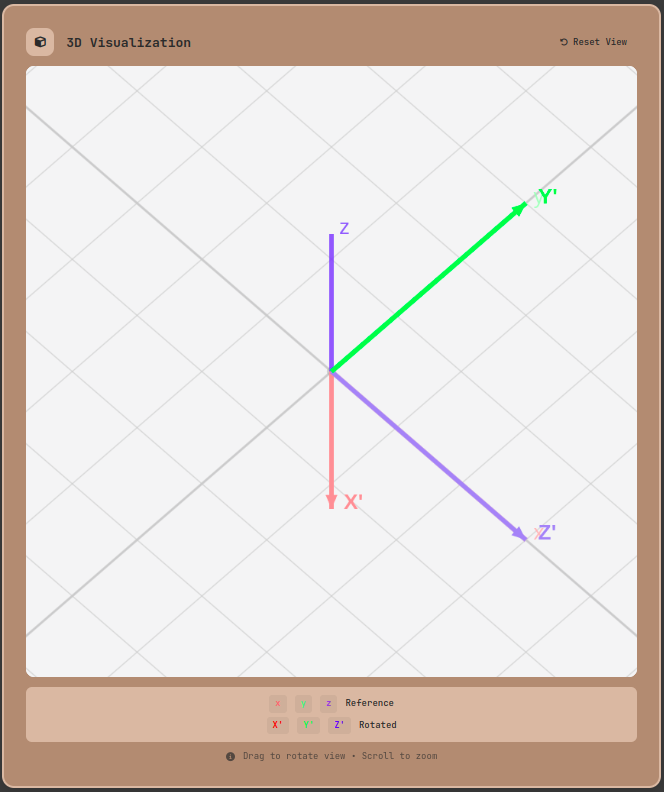
3D Rotation Converter tool: Input settings and interface

4. Use the results:
   • Apply the converted Euler Angles directly to Unity's transform.eulerAngles
   • Synchronize the robotic arm simulation in real-time

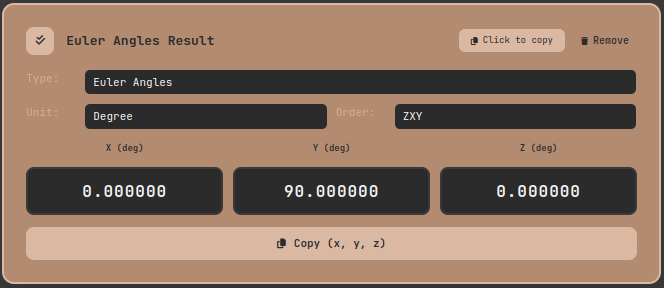
3D Rotation Converter tool: Input settings and interface

The 3D visualization is particularly important in this process. Numbers alone make it hard to verify correctness, but visually confirming the rotated coordinate axes lets you instantly judge whether the orientation is correct.

Solving Real-World Problems: Failures and Breakthroughs

Even with theory and tools, unexpected problems arise in practice. Let's examine problems developers across various fields have actually encountered and how they were solved.

Problem 1: Unnatural Rotation in Animation

Situation: Implementing a feature to rotate a game character to face an enemy

Initial approach: Calculate Euler Angles from two direction vectors and linearly interpolate

# Wrong approach
start_euler = calculate_euler(start_direction)
end_euler = calculate_euler(end_direction)
interpolated = lerp(start_euler, end_euler, t)  # Problem!

Issue: When the character needs to rotate close to 180 degrees, it takes a strange path. Sometimes it even rotates a full 360 degrees.

Solution process:

1. Recognize the limitations of Euler Angle interpolation (can't find the shortest path beyond 180 degrees)
2. Switch to Quaternion SLERP
3. Result: Always smooth rotation along the shortest path

The lesson learned: Use Quaternions whenever interpolation is needed

Problem 2: Unexpected Robot Arm Movement

Situation: Implementing a pick-and-place task with a 6-axis robotic arm

Problem: Works fine in most positions, but near fully extended states, joints suddenly rotate rapidly or take strange paths

Root cause analysis: When the robot arm is fully extended, multiple joint rotation axes align. This state is called a Singularity—similar to how when you fully extend your elbow, it becomes difficult to move your fingertip in certain directions. In this state, even small fingertip movements require large joint rotations.

Solution:

1. Replan the path before the arm becomes fully extended
2. Smoothly interpolate intermediate waypoints to the target position using Quaternions
3. Intentionally maintain a slightly bent posture near singularities

# Simple singularity avoidance example
def move_robot_safely(current_pose, target_pose):
    # Divide the path from current to target into 10 steps
    intermediate_poses = []
    for i in range(10):
        t = i / 10.0
        # Smoothly interpolate with Quaternions
        interpolated = slerp(current_pose, target_pose, t)
        intermediate_poses.append(interpolated)
    
    # Execute each intermediate pose sequentially
    for pose in intermediate_poses:
        move_to_pose(pose)

Result: Smooth, predictable movement while avoiding the dangerous fully-extended posture

Problem 3: Object Jitter in AR Apps

Situation: Placing virtual objects in real space using ARKit

Problem: Objects jitter slightly when the camera moves

Cause:

• Converting Quaternions from ARKit to Euler Angles every frame
• Accumulated floating-point errors
• Sudden value changes near Gimbal Lock

Solution:

1. Modify the rendering pipeline to use Quaternions directly
2. Add filtering (smooth with SLERP using previous values)
3. Normalize Quaternions every frame

// iOS ARKit example
let currentRotation = SCNQuaternion(anchor.transform.rotation)
let smoothed = simd_slerp(previousRotation, currentRotation, 0.3)
let normalized = simd_normalize(smoothed)
node.rotation = normalized

Result: Completely stable object rendering

Performance and Optimization: A Practitioner's Perspective

Even a theoretically perfect solution is useless if it has performance issues. Understanding the performance characteristics of each representation is crucial.

Computational Complexity Comparison

The computational complexity of each representation is reported in academic literature as follows:

According to PMC research "Computationally Efficient 3D Orientation Tracking", Quaternions are more computationally efficient than Matrices when composing multiple rotations in sequence. However, when only single vector transformation is needed, Matrices are more efficient with direct multiplication.

Key insights (from 3D Game Engine Programming, Game Math):

• Quaternion multiplication (28 operations) composes rotations with ~40% fewer operations than Matrix multiplication (45 operations)
• Matrices accumulate orthonormality distortion during repeated operations, requiring periodic re-normalization
• Euler Angles are the slowest due to mandatory trigonometric (sin, cos) calculations

Optimization Checklist

1. Quaternion normalization is essential

Accumulated floating-point errors cause the quaternion to no longer be unit length:

def normalize_quaternion(q):
    norm = np.sqrt(q[0]**2 + q[1]**2 + q[2]**2 + q[3]**2)
    if norm < 1e-10:  # Handle near-zero case
        return np.array([0, 0, 0, 1])  # Identity rotation
    return q / norm

2. Eliminate unnecessary conversions

Round-trip conversions like Euler → Quaternion → Euler amplify errors. Maintain a single representation consistently whenever possible.

3. Hybrid strategy

• User input: Euler Angles (intuitive)
• Internal computation: Quaternion (stable, fast)
• GPU transfer: Matrix (hardware optimized)

Conclusion: A Guide to Making the Right Choice

3D rotation isn't just about memorizing mathematical formulas—it's an engineering judgment call about selecting the right tool for each situation. From my experience:

Use Euler Angles when:

• Building user interfaces (editors, settings screens)
• Humans need to directly understand and adjust values
• Working within limited rotation ranges where Gimbal Lock won't occur

Use Quaternions when:

• Doing real-time animation and interpolation
• Processing and filtering sensor data
• Working with game engines and physics simulations
• Needing stable calculations without singularities

Use Rotation Matrices when:

• Working with graphics pipelines (OpenGL, DirectX)
• Integrating with other transformations like scale and shear
• Needing linear algebra-based optimization

Above all, use tools to verify your work. Validating conversion results with a visual tool like 3D Rotation Converter helps catch countless bugs before they become problems.

For Further Study

1. Ken Shoemake, "Animating Rotation with Quaternion Curves" - The groundbreaking 1985 SIGGRAPH paper that introduced Quaternions to computer graphics
2. James Diebel, "Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors" - A complete reference for conversion mathematics
3. Eigen Library Official Documentation - The standard library for C++ implementation

Rotation transformations are an eternal companion in 3D programming. It's not something you learn once and forget—every project brings new challenges and solutions. I hope this article serves as a small milestone on your journey.